Long Nguyen

The Mandelbrot Set

One of the most beautiful and profound objects in mathematics is the Mandelbrot set. Although the results are deep, they are accessible to anyone with a background in algebra. This post is a broad survey of some these results. I was first introduced to it by my differential equations professor, Bob Devaney. Most of the pictures and all of the programs are written by me in Java using Processing ported to Javascript using ProcessingJS. A few images are from Bob's Mandelbrot Set Explorer website.

Recall that the complex numbers is the set of numbers of the form $a+bi$ where $a,b$ are real numbers and $i$ is the imaginary unit with $i^2=-1$. For example, $2-3i$, $\pi+\sqrt{2}i$, $7=7+0i$, $8i=0+8i$ are complex numbers. A complex number $a+bi$ can be identified with the point $(a,b)$ on the complex plane. In this way, the complex plane is similar to the $xy$-plane from algebra.

Two complex numbers are added component-wise and are multiplied by using the distributive property. For example, $$(2+3i)+(4-i)=6+2i$$ and $$(2+3i)(4-5i)=8-10i+12i-15i^2=23+2i$$ where the last equality is obtained by using $i^2=-1$.

Iteration is the process of repeating something over and over again. In math, often, this process is repeatedly applying a function. To iterate a function is to apply the function over and over again, using the output of the previous application as the input of the next. This is simply composing a function with itself over and over again.

Let $F(x)$ be a function $x_0$ be any complex number. Consider the infinite sequence $$\{x_0, x_1=F(x_0), x_2=F(x_1), x_3=F(x_2), ..., x_n=F(x_{n-1})...\}$$ where each term in the sequence is obtained by applying $F(x)$ to the previous term.

Definition.

The number $x_0$ is called the seed of the iteration. The list of numbers $\{x_0,x_1,x_2...\}$ is called the orbit of $x_0$ under the iteration of $F(x)$.

For the Mandelbrot set, we are interested in the function $F(x)=x^2+c$ where $c$ is a complex constant. For each complex number $c$, we analyze fate of the orbit of the seed $x_0=0$ under the iteration of $F(x)$. Let's look at some examples.

Example 1

Let $c=1$ so that $F(x)=x^2+c=x^2+1.$

Consider the seed $x_0=0$.

$x_1=F(x_0)=F(0)=0^2+1=1$

$x_2=F(x_1)=F(1)=1^2+1=2$

$x_3=F(2)=2^2+1=5$

$x_4=F(5)=5^2+1=26$

We note that the numbers, $x_i$, in this sequence gets bigger and bigger and this orbit tends to infinity.

Example 2

Let $c=i$ so that $F(x)=x^2+c=x^2+i.$

As before, let $x_0=0$.

$x_1=F(x_0)=F(0)=0^2+i=i$

$x_2=F(x_1)=F(i)=i^2+i=-1+i$

$x_3=F(-1+i)=(-1+i)^2+i=1-2i+i^2+i=-i$

$x_4=F(-i)=(-i)^2+i=-1+i$

We note that this orbit goes back and forth between $-i$ and $-1+i$ and does not tend to infinity. In this case, we say that the orbit is a 2-cycle. In general, if an orbit periodically cycles between $n$ distinct numbers, we call that orbit an n-cycle.

To define the Mandelbrot set, we just need to note a simple observation. For any complex number $c$, under the iteration of $F(x)=x^2+c$, the orbit of the seed $x_0=0$ either goes to infinity, or it does not.

Now we are ready to define the Mandelbrot set.

Definition. The Mandelbrot set.

Let $c$ be a complex number. Then, $c$ is in the Mandelbrot set $M$ if the orbit of $0$ under the iteration of $F(x)=x^2+c$ does not go to infinity.

In Example 1 above, when $c=1$, we saw that the orbit of $0$ under the iterations of $F(x)=x^2+c=x^2+1$ tends to infinity. Thus, $c=1$ is not in the Mandelbrot set. But in Example 2, if $c=i$, the orbit of $0$ under $F(x)=x^2+i$ is a 2-cycle and therefore does not tend to infinity. So $c=i$ is in the Mandelbrot set.

We now "paint" the Mandelbrot set by coloring every complex number by the following rules:

1. Color a complex number $c$ black if $c$ is in $M$, that is, if the orbit of $0$ under iteration of $F(x)=x^2+c$ does NOT go to infinity.
2. Color $c$ white if $c$ is not in $M$ and the orbit of $0$ under iteration of $F(x)$ does go to infinity.

Although the rules above seem simple, you might notice that they are, in practice, hard to implement. How do we know if a particular orbit tends to infinity if we can't generate an infinite sequence? A sequence that stays locally around a neighborhood of the origin for the first 1000 iterations might leave that neighborhood for infinity thereafter. Conversely, a sequence that shoots off to infinity might loop back to a small neighborhood of the origin at some future iteration.

The following two results, stated without proofs, will help simplify some of our calculations.

Theorem 1

The Mandelbrot set lies within the circle of radius $2$ centered at the origin.

Theorem 2. The Escape Criterion.

If the orbit of $x_0=0$ under iteration of $F(x)=x^2+c$ leaves the circle of radius $2$ centered at the origin, then orbit will tend to infinity and $c$ is not in the Mandelbrot set.

With these theorems, it is easy to implement an algorithm that reasonably approximate a painting of the Mandelbrot set. For each complex number $c$, iterate $F(x)$ until either 1) the orbit leaves the circle of radius $2$ centered at the origin and color $c$ white or 2) the number of iteration hits a predefined maximum value(40 is a good value) and we color it black.

Finally, here is a picture of the Mandelbrot set. Click anywhere to zoom in. Press SPACEBAR or ENTER to reset.

Mandelbrot Set Zoom

Because the maximum iteration is only $40$, the program above does not reveal the fine details under increasing magnification that the Mandelbrot set deserved. Please click here to see a great Mandelbrot set zoom written in Javascript. Instead of coloring points not on the Mandelbrot set white, I color it according to how how fast it leaves for infinity. Here, infinity is the region outside the circle of radius $2$ by the Escape Criterion. Yellow points, for example, take the longest to reach infinity(more than 30 iterations) while red points take the least number of iterations(less than 5).

If you experiment with the program linked above, you see that the set is quasi-self-similar in that smaller, but different versions of itself can be found both on the boundary of the main cardioid as well as "floating" on long, thin spokes at arbitrarily small scales.

For those familiar with topology, the Mandelbrot set is closed and bounded, hence compact. It is also connected. For a proof of its connectedness, see here. It is still an open question whether it is locally connected.

Definition

The largest region on the Mandelbrot set is a cardioid called the main cardioid. Attached to this cardioid are decorations called primary decorations or primary bulbs. Each primary decoration has a main antenna, which consists of a number of spokes. If a primary decoration has $n$ spokes, we call the decoration a period $n$ primary decoration.

Examples. Period 3,4 and 7 primary bulbs.

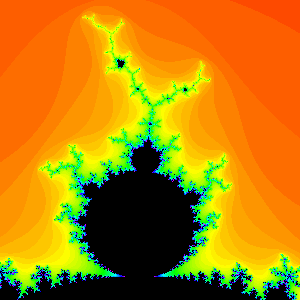
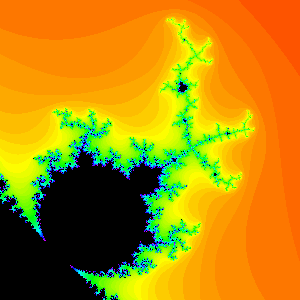
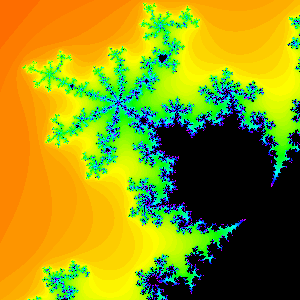
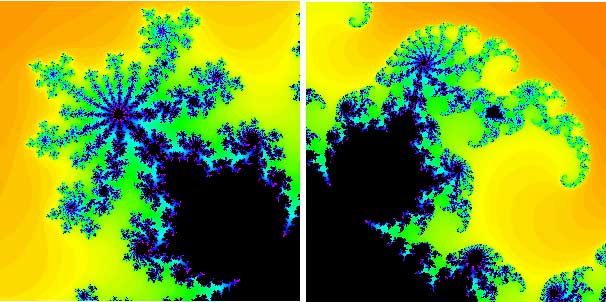
Bulbs with the same period may look very different. Both of the following primary bulbs are period 12 bulbs.

Examples. Two period 12 primary bulbs.

The following two theorems give us some insights into the intricate structure of the Mandelbrot set.

Theorem 3

Let $n$ be any positive integer. There is a primary decoration with period $n$.

Theorem 4

Let $c$ be a complex number in the interior of a period $n$ primary decoration. The orbit of $0$ under iteration of $F(x)=x^2+c$ will tend to an $n$-cycle.

Theorem 3 says that the periods of the primary bulbs span the entire set of positive integers. For example, there is a primary bulb with 23,491 spokes. Moreover, for any complex number $c$ inside of that bulb, the the orbit of $0$ under iteration of $F(x)=x^2+c$ will tend to a 23,491-cycle! I can't show a bulb with that many spokes. But here is one with 23.

You can find all integer period bulbs in an area known as the Seahorse Valley just to the left of the main cardiod, pictured below.

The Mandelbrot set arises from the study of complex dynamical systems. Under iterative systems, typically, behaviors can quickly become chaotic and unpredictable, even for simple functions. It is amazing that the Mandelbrot set exhibits such periodic and predictable behaviors in the interior of the primary bulbs. Even more surprising is how those behaviors are tied to such simple geometric properties of the set, in this case, the number of spokes on primary bulbs.

To see more interesting properties of the Mandelbrot set, let's look at the idea of a Julia set.

Definition. The Julia set.

Let $c$ be a complex number. The filled Julia set of $c$, denoted $J_c$, is the set of all seeds $x_0$ whose orbits do not go to infinity under iterations of $F(x)=x^2+c$.

Notice the difference between the Julia set and the Mandelbrot set. The Mandelbrot is one set. It is the set of all complex numbers $c$ whose orbits of the seed $0$ do not go to infinity under iterations of $F(x)=x^2+c$. There is a filled Julia set $J_c$ for each complex number $c$. Fix a $c$. A complex number $x_0$ whose orbit under $F(x)=x^2+c$ does not go to infinity is an element of $J_c$. Thus, there is a different Julia set $J_c$ for each $c$.

In the Mandelbrot set, we fix the seed $0$ and consider the set of all complex numbers $c$ whose orbits of $0$ do not go to infinity. In the Julia set, we fix a complex number $c$ and consider the set of all seeds $x_0$ whose orbit do not go to infinity. Let's do some examples.

Example 4

Let $c=i$ so that $F(x)=x^2+i.$

Let $x_0=0$.

$x_1=F(x_0)=F(0)=0^2+i=i$

$x_2=F(x_1)=F(i)=i^2+i=-1+i$

$x_3=F(-1+i)=(-1+i)^2+i=1-2i+i^2+i=-i$

$x_4=F(-i)=(-i)^2+i=-1+i$

This example was used earlier in Example 2 to show that $i$ is in the Mandelbrot set since the orbit of $0$ does not go to infinity. This example show also that $0$ is in $J_i$, the filled Julia set of $c=i$. Notice from above calculation that the orbits of the seeds $x_0=i,-1+i,-i$ also do not tend to infinity. We can thus conclude that $i,-1+i,-i$ are all in $J_i$.

The following three pictures show the Julia set for various values of $c$.

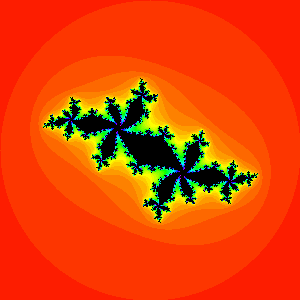
Theorem 4. The Fundamental Dichotomy.

Let $c$ be a complex number. If $c$ is in the Mandelbrot set then the Julia set $J_c$ is a connected(one piece) set. If $c$ is not in the Mandelbrot set, then the Julia set $J_c$ is an infinite, totally disconnected set.

In the following Processing program, if you move your mouse cursor over a point $c$ in the complex plane on the left window, the right window shows the corresponding filled Julia set $J_c$. Test the Fundamental Dichotomy theorem by moving the cursor in and out of the Mandelbrot set.

What do you notice when you move your cursor on each of the primary bulbs?

Definition. Rotation Numbers.

To each primary decoration, we will attach a fraction $\dfrac{p}{q}$ called the rotation number of the decoration. The denominator $q$ is simply the period of the bulb. The numerator $p$ can be computed in several ways.

1. A period $q$ primary bulb has $q$ spokes. The spoke that comes directly from the main body of the bulb is called the principal spoke. The smallest spoke is $p^{th}$ spoke counted counterclockwise from the principal spoke.
2. The filled Julia set for a period $q$ primary bulb has junction points, each of which has $q$ "ears". The largest ear is the principal ear. The smallest ear is $p^{th}$ spoke counted counterclockwise from the principal ear.

What is the rotation number for the following primary bulb?

Can you see why the rotation is $\dfrac{1}{4}$? Since the bulb has $4$ spokes, $q=4$. Using the first method, notice that the smallest spoke is the first spoke counted counterclockwise from the principal spoke. Thus $p=1$. Using the second method, we note that the smallest ear is the first ear counted counterclockwise from the principal, largest ear. Below is another example. Its rotation number is $\dfrac{3}{7}$. Can you see why?

Farey Addition.

Given two reduced fractions, $\dfrac{a}{b}$ and $\dfrac{c}{d}$, their farey sum is $$\dfrac{a}{b}+\dfrac{c}{d}=\dfrac{a+c}{b+d}.$$

Example.

$$\dfrac{1}{3}+\dfrac{2}{5}=\dfrac{3}{8}.$$

Let's be honest, this is how we all wanted to add fractions back in elementary school! Although Farey addition seems silly, it has many applications including clocks, gear ratios, approximations, and an interesting connection to the Riemann Hypothesis. You can read all about these applications in this wonderful paper The Farey Sequence.

It's easy to show the following.

Lemma.

The farey sum of two fractions lie between them. More precisely, if $\dfrac{a}{b}<\dfrac{c}{d}$ then $$\dfrac{a}{b}<\dfrac{a+c}{b+d}<\dfrac{c}{d}.$$

Theorem.

Given two primary bulbs, the rotation number of the largest bulb between them can be found by using Farey addition.

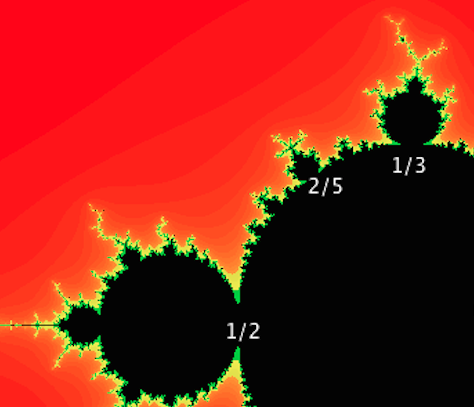
In the above picture, the $\dfrac{2}{5}$ primary bulb is the largest bulb between the $\dfrac{1}{2}$ and $\dfrac{1}{3}$ bulbs and $$\dfrac{1}{2}+\dfrac{1}{3}=\dfrac{2}{5}.$$

Theorem.

The set of rotation numbers on the primary decorations of the Mandelbrot set is exactly the set of rational numbers in the interval $[0,1]$. In addition, the rotation numbers of the primary bulbs starting at the cusp of the main cardioid and traversing counterclockwise form the exact same order as the rational numbers in $[0,1]$.

Here's a picture with some of the rotation numbers labelled.

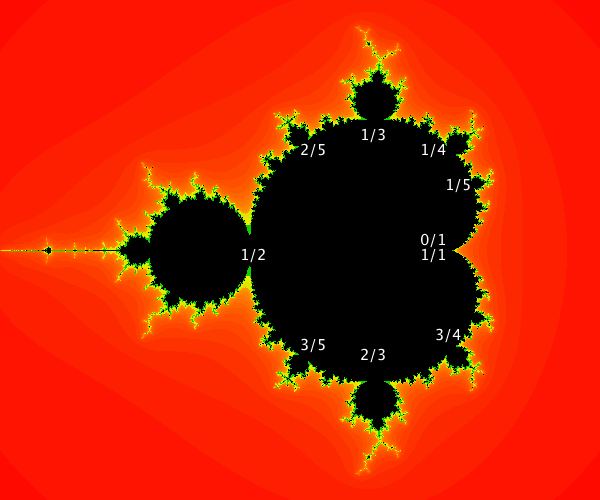
Farey addition described above can be used to find well-known sequences on the Mandlebrot set. Can you use it to find the following sequences?

1. Positive integers: $\{1,2,3,...\}$.
2. Odd integers: $\{1,3,5,7...\}$.
3. Fibonacci sequence: $\{2,3,5,8,13...\}$.

Hopefully, you're convinced that the Mandelbrot set is an incredible geometric object. It arises out of simple iterations of a quadratic function that you learn in high school yet its intricate structures are still not well understood. The proof of many of the theorems mentioned here required advanced mathematical tools in topology and complex analysis. But its beauty can still be widely appreciated. I hope you enjoy this very broad introduction to the set. Thanks for reading!